Dr. Jack Wetherell
Research and Development Scientist
Research and Development
Imagineering
Founded by Walt Disney in 1952, Walt Disney Imagineering is the creative force behind the memorable Disney experiences that connect and inspire across generations and borders. And we are proud our experiences continue to set the bar in an industry Walt’s “Imagineers” pioneered. Walt Disney Imagineering embodies a world-class design firm, premier development company, extraordinary storytelling studio, and cutting-edge innovation lab — all rolled into one. Home to an overwhelming breadth of expert talent from around the globe, Imagineers partner closely with colleagues from across The Walt Disney Company to bring the most awe-inspiring new worlds and cherished characters to life.
Autonomous Vehicles
I currently work as a machine learning data scientist at Humn AI. My role is to develop machine learning models to quantify and predict the environmental and behavioral risks generated by fleets of autonomous vehicles. I deploy many types of real-world automated driving systems in state-of-the-art simulators in a range of diverse scenarios, in order to generate risk profiles of the vehicles, and learn how these couple to the environmental effects. This allows me to train machine learning models that can couple the environmental features of a vehicle to its driving events that produce risk, unique to self-driving systems. These models are built using industry-leading technologies and frameworks. Producing these machine-learned models of autonomous vehicle risk has allowed me to deepen my experience in the implementation of deep learning and classical machine learning methods, using TensorFlow, Keras, PyTorch, Cuda, and sklearn. In addition, due to the large scale nature of the data, I have applied many machine learning training, versioning, management and deployment tools such as ML Flow, CI, AWS (EC2 deployment and s3 hosting), git, DVC, and GPU model deployment.
In addition, I have worked to develop HumnPilot, our custom-built self-driving car software system. This allows me to fully understand the self-driving
software stack as I have implemented them directly in C++ and python. More specifically, this allows our team to have total control over the behavior of
the driving system and allows us to determine which components of the system are responsible for particular risks. I also entered the Waymo motion prediction
competition, where the goal was to develop a deep learning model that could predict the motion of real vehicles from sensor data, using the extensive Waymo open
dataset. I developed a custom rasterization-based convolutional neural network (CNN) method that considered time as a channel of a high-dimensional image.
My method came in 13th place at the end of the competition, out of several hundred entrants. Training this model on a huge dataset (~5TB compressed) on a
V100 GPU allowed me to gain invaluable experience in optimizing machine learning pipelines, ensuring no bottlenecks are present, and maximizing GPU utilization.
I also have taken part and completed the Udacity Self-Driving Car Engineer Nanodegree. In this six-month intensive distance learning program, led by world experts in the field such as Sebastian Thrun (the creator of the DARPA Grand Challenge winner Stanley), and Vincent Vanhoucke (the principal scientist at Google Brain), I learned how to write the computer vision and machine learning code required to program a self-driving car. In this project-based nanodegree, I learned more advanced concepts in computer vision, object recognition, filtering, deep learning, convolutional and fully convolutional neural networks, behavioral cloning, sensor fusion, and how to integrate these methods with robotics systems using ROS (robot operating system).
I also am responsible for training new members of the data science team on the topics of machine learning and computational skills related to our research projects involving autonomous vehicles. I give regular pedological talks on our machine learning methods and autonomous vehicle research to both technical and non technical members of the wider company and to external collaborators.
Quantum Technologies
Many of my current projects involve integrating modern machine learning approaches, such as convolutional neural networks (CNNs), to inform the development of new methods in condensed matter physics. Our general aim is to train machine learning models to learn the fundamental properties of important but difficult to approximate quantities such as the single-particle reduced density matrix, and thus we can gain insight at a deep level, to what features are the most crucial and how we can describe them in a way that is the most amenable to approximation. We have recently completed work into building functionals and gaining insights into the single-particle reduced density matrix using deep learning [J. Wetherell et al. Royal Society of Chemistry Faraday Discussions (2020)].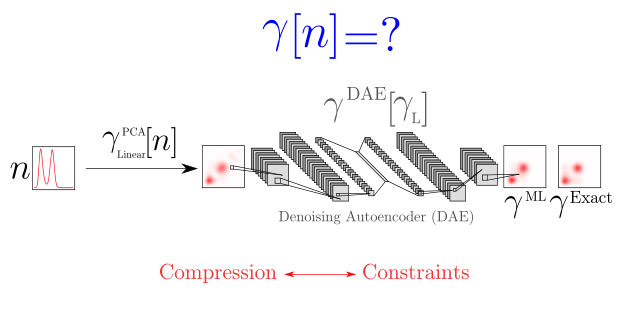
I also organsied the 2021 GDR REST Machine Learning Discussion Meeting in Palaiseau, and my introductory talk on the basics of machine learning can be found on YouTube:
Many-Body Perturbation Theory
One of my main branches of research involve investigating existing, and developing novel, corrections to methods within Many-Body Perturbation Theory (MBPT). MBPT is an intuitive theory that describes how a system responds when electrons are added and removed, with central concepts of the many-body Green's function and screened interaction. To date we are investigating the effect of the many flavors of the GW approximation on the electron density, associated Kohn-Sham potentials and quasi-particle energies by comparing to the exact quantities.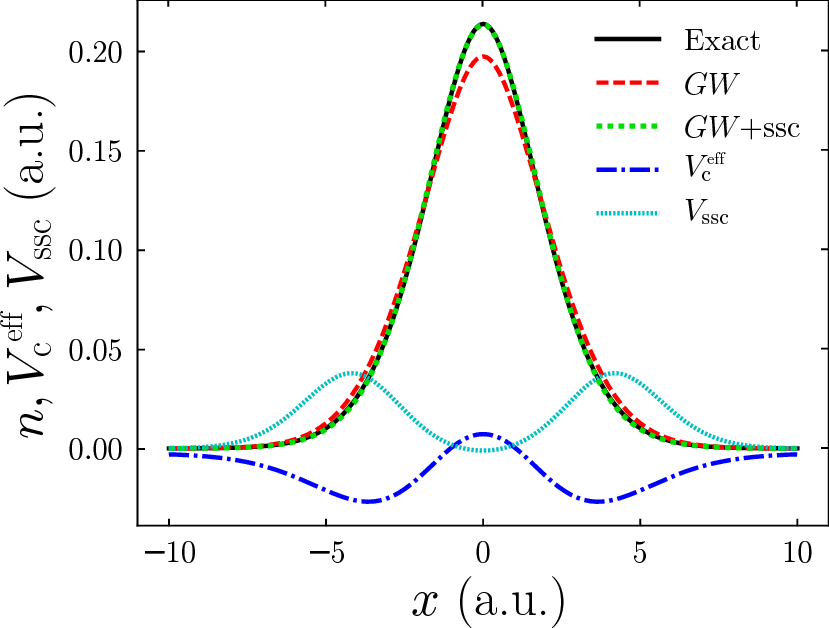
We are currenty using this to develop models of
the electron screening that capture the correct behavior of the most well-performing GW flavors, without
the onerous computation cost they entail. Thus far we have developed a novel vertex correction to the self-energy within a GW calculation that eliminates the unwanted effect of the
well-known self-screening error with a very small additional computational cost [J. Wetherell et al.
Physical Review B (Rapid Communications) 97 121102(R) (2018)].
We have also used these model systems to illustrate that, unlike Kohn-Sham density functional theory, many-body perturbation theory methods such as Hartree-Fock and the GW approximation exhibit Kohn’s concept of nearsightedness [J. Wetherell et al. Physical Review B 99 045129 (2019)]. This means that the potential describing one subsystem needs not contain any additional features due to the presence of surrounding subsystems. See the following video (first presented at the ETSF Young Researcher's Meeting 2019) for an in-depth discussion of this branch of research:
Time-Dependent Density Functional Theory
One of the fundamental challenges of TDDFT is approximating the Kohn-Sham (KS) exchange-correlation (xc) potential. We have shown that LDAs (Local Density Approximations) to the xc potential can be constructed in finite systems from 'slab-like' systems of 1, 2 and 3 electrons [M. T. Entwistle et al. Physical Review B 94 205134 (2016)]. We showed that these local approximations when applied adiabatically as the time-dependent exchange-correlation potential perform very poorly for the time-dependent density in a dynamic tunnelling system. We have learned from our work in MBPT that this is predominantly due to the lack of ‘nearsightedness’; an advantageous property that each electron is only effected by features of the fictitious potential in its own vicinity. Subsequently we construct a nearsighted form of generalised TD-KS theory based on unrestricted Hartree-Fock theory. [M. J. P. Hodgson and J. Wetherell. Physical Review A 101 032502 (2020)]. We find simple approximations to our approach (we term our new approximation the ULDA+) give greatly improved electronic properties when applied to exactly-solvable model molecules, as they are required to capture far less complex physical phenomena.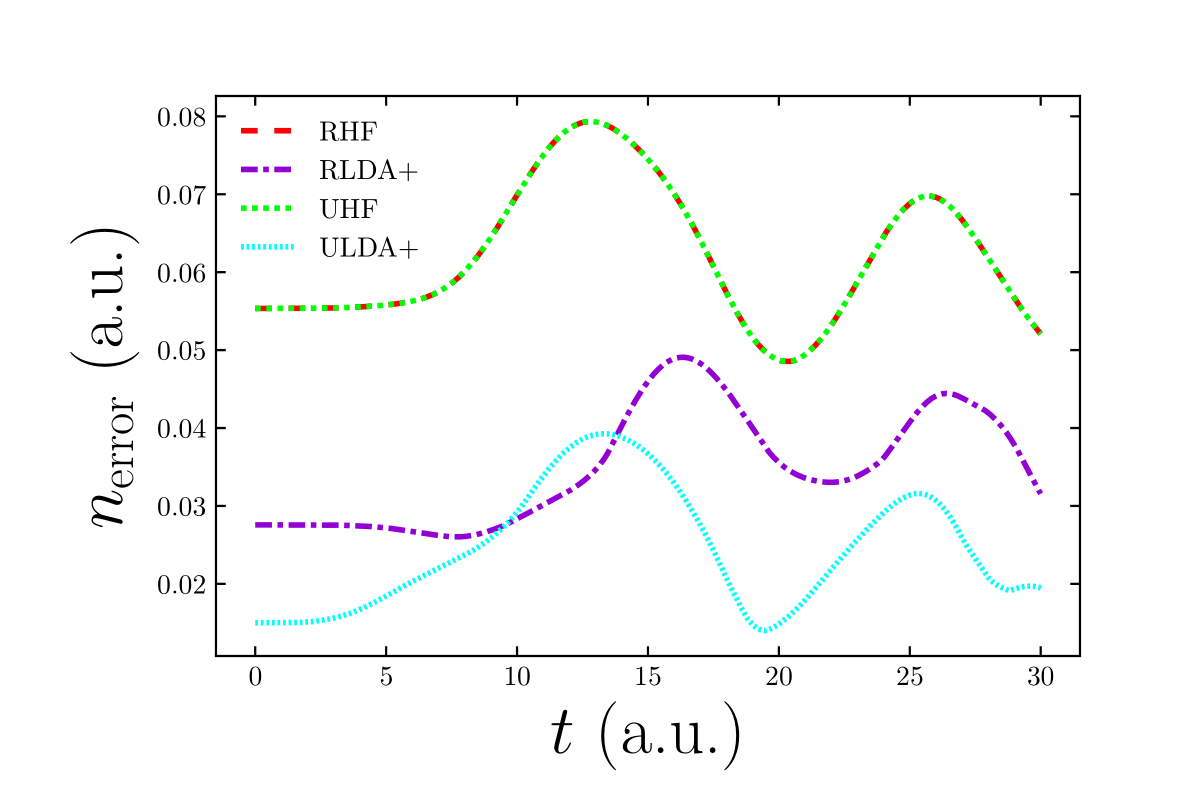
The improvements this novel theory provides can be used to accelerate the rapid development of cutting-edge molecular technologies.
Hybrid Functionals
Hybrid functionals are usually considered the meeting point between DFT (LDA or PBE etc) and MBPT (Hartree-Fock). By mixing these potentials together via a linear mixing parameter one can generate more accurate results than the individual methods alone.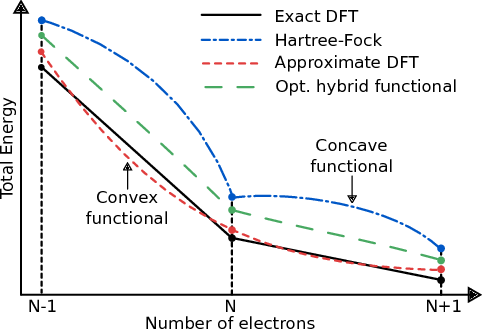
We explored the effect of determining the mixing parameter via enforcing Koopermans' condition to hold in
our model systems. We show that this method yields strikingly accurate densities [A. R. Elmaslmane and
J. Wetherell et al. Physical Review Materials (Rapid Communication) 2 040801(R) (2018)].
Founded by Walt Disney in 1952, Walt Disney Imagineering is the creative force behind the memorable Disney experiences that connect and inspire across generations and borders. And we are proud our experiences continue to set the bar in an industry Walt’s “Imagineers” pioneered. Walt Disney Imagineering embodies a world-class design firm, premier development company, extraordinary storytelling studio, and cutting-edge innovation lab — all rolled into one. Home to an overwhelming breadth of expert talent from around the globe, Imagineers partner closely with colleagues from across The Walt Disney Company to bring the most awe-inspiring new worlds and cherished characters to life.
Autonomous Vehicles
I currently work as a machine learning data scientist at Humn AI. My role is to develop machine learning models to quantify and predict the environmental and behavioral risks generated by fleets of autonomous vehicles. I deploy many types of real-world automated driving systems in state-of-the-art simulators in a range of diverse scenarios, in order to generate risk profiles of the vehicles, and learn how these couple to the environmental effects. This allows me to train machine learning models that can couple the environmental features of a vehicle to its driving events that produce risk, unique to self-driving systems. These models are built using industry-leading technologies and frameworks. Producing these machine-learned models of autonomous vehicle risk has allowed me to deepen my experience in the implementation of deep learning and classical machine learning methods, using TensorFlow, Keras, PyTorch, Cuda, and sklearn. In addition, due to the large scale nature of the data, I have applied many machine learning training, versioning, management and deployment tools such as ML Flow, CI, AWS (EC2 deployment and s3 hosting), git, DVC, and GPU model deployment.
In addition, I have worked to develop HumnPilot, our custom-built self-driving car software system. This allows me to fully understand the self-driving
software stack as I have implemented them directly in C++ and python. More specifically, this allows our team to have total control over the behavior of
the driving system and allows us to determine which components of the system are responsible for particular risks. I also entered the Waymo motion prediction
competition, where the goal was to develop a deep learning model that could predict the motion of real vehicles from sensor data, using the extensive Waymo open
dataset. I developed a custom rasterization-based convolutional neural network (CNN) method that considered time as a channel of a high-dimensional image.
My method came in 13th place at the end of the competition, out of several hundred entrants. Training this model on a huge dataset (~5TB compressed) on a
V100 GPU allowed me to gain invaluable experience in optimizing machine learning pipelines, ensuring no bottlenecks are present, and maximizing GPU utilization.
I also have taken part and completed the Udacity Self-Driving Car Engineer Nanodegree. In this six-month intensive distance learning program, led by world experts in the field such as Sebastian Thrun (the creator of the DARPA Grand Challenge winner Stanley), and Vincent Vanhoucke (the principal scientist at Google Brain), I learned how to write the computer vision and machine learning code required to program a self-driving car. In this project-based nanodegree, I learned more advanced concepts in computer vision, object recognition, filtering, deep learning, convolutional and fully convolutional neural networks, behavioral cloning, sensor fusion, and how to integrate these methods with robotics systems using ROS (robot operating system).
I also am responsible for training new members of the data science team on the topics of machine learning and computational skills related to our research projects involving autonomous vehicles. I give regular pedological talks on our machine learning methods and autonomous vehicle research to both technical and non technical members of the wider company and to external collaborators.
Quantum Technologies
Many of my current projects involve integrating modern machine learning approaches, such as convolutional neural networks (CNNs), to inform the development of new methods in condensed matter physics. Our general aim is to train machine learning models to learn the fundamental properties of important but difficult to approximate quantities such as the single-particle reduced density matrix, and thus we can gain insight at a deep level, to what features are the most crucial and how we can describe them in a way that is the most amenable to approximation. We have recently completed work into building functionals and gaining insights into the single-particle reduced density matrix using deep learning [J. Wetherell et al. Royal Society of Chemistry Faraday Discussions (2020)].
I also organsied the 2021 GDR REST Machine Learning Discussion Meeting in Palaiseau, and my introductory talk on the basics of machine learning can be found on YouTube:
Many-Body Perturbation Theory
One of my main branches of research involve investigating existing, and developing novel, corrections to methods within Many-Body Perturbation Theory (MBPT). MBPT is an intuitive theory that describes how a system responds when electrons are added and removed, with central concepts of the many-body Green's function and screened interaction. To date we are investigating the effect of the many flavors of the GW approximation on the electron density, associated Kohn-Sham potentials and quasi-particle energies by comparing to the exact quantities.
We are currenty using this to develop models of
the electron screening that capture the correct behavior of the most well-performing GW flavors, without
the onerous computation cost they entail. Thus far we have developed a novel vertex correction to the self-energy within a GW calculation that eliminates the unwanted effect of the
well-known self-screening error with a very small additional computational cost [J. Wetherell et al.
Physical Review B (Rapid Communications) 97 121102(R) (2018)]. We have also used these model systems to illustrate that, unlike Kohn-Sham density functional theory, many-body perturbation theory methods such as Hartree-Fock and the GW approximation exhibit Kohn’s concept of nearsightedness [J. Wetherell et al. Physical Review B 99 045129 (2019)]. This means that the potential describing one subsystem needs not contain any additional features due to the presence of surrounding subsystems. See the following video (first presented at the ETSF Young Researcher's Meeting 2019) for an in-depth discussion of this branch of research:
Time-Dependent Density Functional Theory
One of the fundamental challenges of TDDFT is approximating the Kohn-Sham (KS) exchange-correlation (xc) potential. We have shown that LDAs (Local Density Approximations) to the xc potential can be constructed in finite systems from 'slab-like' systems of 1, 2 and 3 electrons [M. T. Entwistle et al. Physical Review B 94 205134 (2016)]. We showed that these local approximations when applied adiabatically as the time-dependent exchange-correlation potential perform very poorly for the time-dependent density in a dynamic tunnelling system. We have learned from our work in MBPT that this is predominantly due to the lack of ‘nearsightedness’; an advantageous property that each electron is only effected by features of the fictitious potential in its own vicinity. Subsequently we construct a nearsighted form of generalised TD-KS theory based on unrestricted Hartree-Fock theory. [M. J. P. Hodgson and J. Wetherell. Physical Review A 101 032502 (2020)]. We find simple approximations to our approach (we term our new approximation the ULDA+) give greatly improved electronic properties when applied to exactly-solvable model molecules, as they are required to capture far less complex physical phenomena.
The improvements this novel theory provides can be used to accelerate the rapid development of cutting-edge molecular technologies.
Hybrid Functionals
Hybrid functionals are usually considered the meeting point between DFT (LDA or PBE etc) and MBPT (Hartree-Fock). By mixing these potentials together via a linear mixing parameter one can generate more accurate results than the individual methods alone.
We explored the effect of determining the mixing parameter via enforcing Koopermans' condition to hold in
our model systems. We show that this method yields strikingly accurate densities [A. R. Elmaslmane and
J. Wetherell et al. Physical Review Materials (Rapid Communication) 2 040801(R) (2018)].